Gcf Of 36 And 64

GCF of 36 and 64

GCF of 36 and 64 is the largest possible number that divides 36 and 64 exactly without whatever remainder. The factors of 36 and 64 are ane, 2, 3, 4, 6, nine, 12, 18, 36 and 1, 2, 4, 8, 16, 32, 64 respectively. In that location are three unremarkably used methods to find the GCF of 36 and 64 - Euclidean algorithm, prime factorization, and long division.

one.	GCF of 36 and 64
2.	Listing of Methods
3.	Solved Examples
4.	FAQs

What is GCF of 36 and 64?

Answer: GCF of 36 and 64 is 4.

Caption:

The GCF of two not-zero integers, x(36) and y(64), is the greatest positive integer m(4) that divides both x(36) and y(64) without whatsoever remainder.

Methods to Discover GCF of 36 and 64

The methods to find the GCF of 36 and 64 are explained below.

• Listing Common Factors
• Long Division Method
• Using Euclid's Algorithm

GCF of 36 and 64 past Listing Common Factors

• Factors of 36: 1, 2, 3, four, half dozen, 9, 12, 18, 36
• Factors of 64: 1, 2, 4, viii, sixteen, 32, 64

At that place are 3 common factors of 36 and 64, that are 1, 2, and 4. Therefore, the greatest common factor of 36 and 64 is four.

GCF of 36 and 64 by Long Division

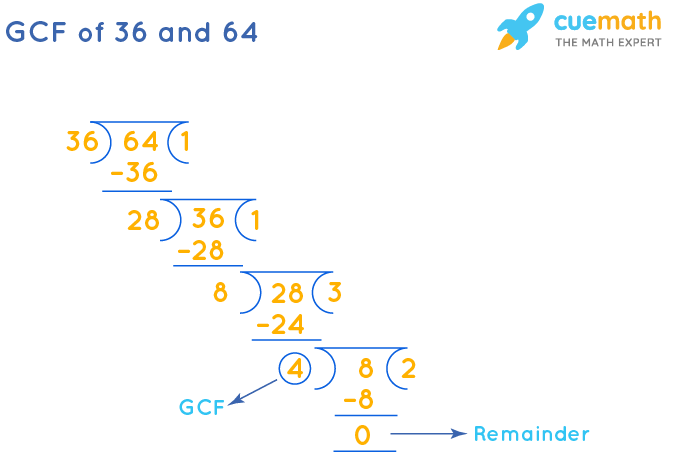
GCF of 36 and 64 is the divisor that we get when the residual becomes 0 later doing long division repeatedly.

• Pace 1: Divide 64 (larger number) by 36 (smaller number).
• Step 2: Since the remainder ≠ 0, we will divide the divisor of step i (36) past the rest (28).
• Step 3: Repeat this process until the residue = 0.

The respective divisor (4) is the GCF of 36 and 64.

GCF of 36 and 64 by Euclidean Algorithm

As per the Euclidean Algorithm, GCF(X, Y) = GCF(Y, X mod Y)
where X > Y and modern is the modulo operator.

Here X = 64 and Y = 36

• GCF(64, 36) = GCF(36, 64 mod 36) = GCF(36, 28)
• GCF(36, 28) = GCF(28, 36 mod 28) = GCF(28, eight)
• GCF(28, 8) = GCF(8, 28 modernistic 8) = GCF(8, iv)
• GCF(viii, 4) = GCF(4, viii mod four) = GCF(4, 0)
• GCF(4, 0) = 4 (∵ GCF(X, 0) = |X|, where 10 ≠ 0)

Therefore, the value of GCF of 36 and 64 is 4.

☛ Also Bank check:

• GCF of 30 and 54 = half-dozen
• GCF of xxx and 70 = ten
• GCF of fifteen and 28 = 1
• GCF of 35 and 63 = seven
• GCF of 32 and 36 = 4
• GCF of 39 and 65 = 13
• GCF of 86 and 42 = 2

GCF of 36 and 64 Examples

1. Instance one: Find the GCF of 36 and 64, if their LCM is 576.

   Solution:

   ∵ LCM × GCF = 36 × 64
   ⇒ GCF(36, 64) = (36 × 64)/576 = 4
   Therefore, the greatest common factor of 36 and 64 is four.

2. Instance 2: Find the greatest number that divides 36 and 64 exactly.

   Solution:

   The greatest number that divides 36 and 64 exactly is their greatest common factor, i.east. GCF of 36 and 64.
   ⇒ Factors of 36 and 64:

   • Factors of 36 = 1, two, 3, 4, 6, 9, 12, 18, 36
   • Factors of 64 = 1, ii, iv, 8, sixteen, 32, 64

   Therefore, the GCF of 36 and 64 is 4.

3. Instance 3: For ii numbers, GCF = 4 and LCM = 576. If i number is 64, find the other number.

   Solution:

   Given: GCF (x, 64) = 4 and LCM (x, 64) = 576
   ∵ GCF × LCM = 64 × (10)
   ⇒ ten = (GCF × LCM)/64
   ⇒ x = (4 × 576)/64
   ⇒ ten = 36
   Therefore, the other number is 36.

become to slidego to slidego to slide

Set to see the world through math'southward eyes?

Math is at the core of everything we practice. Savor solving existent-world math issues in live classes and become an good at everything.

Volume a Complimentary Trial Class

FAQs on GCF of 36 and 64

What is the GCF of 36 and 64?

The GCF of 36 and 64 is 4 . To summate the greatest common factor (GCF) of 36 and 64, we need to factor each number (factors of 36 = ane, 2, 3, four, 6, 9, 12, xviii, 36; factors of 64 = 1, 2, four, eight, 16, 32, 64) and choose the greatest gene that exactly divides both 36 and 64, i.e., 4.

If the GCF of 64 and 36 is 4, Detect its LCM.

GCF(64, 36) × LCM(64, 36) = 64 × 36
Since the GCF of 64 and 36 = iv
⇒ 4 × LCM(64, 36) = 2304
Therefore, LCM = 576
☛ GCF Estimator

What is the Relation Betwixt LCM and GCF of 36, 64?

The following equation can be used to express the relation between Least Common Multiple (LCM) and GCF of 36 and 64, i.e. GCF × LCM = 36 × 64.

What are the Methods to Discover GCF of 36 and 64?

In that location are iii unremarkably used methods to find the GCF of 36 and 64.

• By Prime Factorization
• By Euclidean Algorithm
• Past Long Partition

How to Find the GCF of 36 and 64 past Prime Factorization?

To discover the GCF of 36 and 64, we will find the prime factorization of the given numbers, i.eastward. 36 = ii × ii × iii × 3; 64 = ii × 2 × ii × 2 × two × 2.
⇒ Since two, ii are common terms in the prime factorization of 36 and 64. Hence, GCF(36, 64) = two × two = 4
☛ What is a Prime Number?

How to Find the GCF of 36 and 64 past Long Partition Method?

To find the GCF of 36, 64 using long segmentation method, 64 is divided by 36. The corresponding divisor (4) when remainder equals 0 is taken as GCF.

Gcf Of 36 And 64,

Source: https://www.cuemath.com/numbers/gcf-of-36-and-64/

Posted by: bryanttretind.blogspot.com

Share this post